用抽样方法进行研究时,必然存在抽样误差。率的抽样误差大小可用率的标准误来表示,计算公式如下:
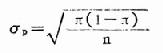
式中:σp为率的标准误,π为总体阳性率,n为样本含量。因为实际工作中很难知道总体阳性率π,故一般采用样本率p 来代替,而上式就变为
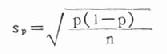
例 20.5河北省组织高碘地方性甲状腺肿流行病学调查,作者调查了饮用不同碘浓度井水居民甲状腺肿的患病情况,其中有两组资料如下表,试分别求出率的标准误。
| 水中含碘量均数(μg/L) | 受检人数 | 患病人数 | 患病率(%) |
| 458.25 | 3315 | 59 | 1.78 |
| 825.95 | 3215 | 180 | 5.60 |
计算法:第一组:n1=3315,p1=1.78%=0.0178
1-p1=1-0.0178=0.9822
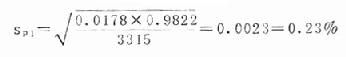
第二组:n2=3215,p2=5.60%=0.056
1-p2=1-0.056=0.944
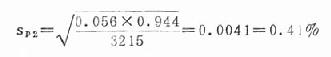
由于样本率与总体率之间存在着抽样误差,所以也需根据样本率来推算总体率所在的范围,根据样本含量n和样本率P的大小不同,分别采用下列两种方法:
(一)正态近似法
当样本含量n足够大,且样本率P和(1-p)均不太小,如np或n(1-p)均≥5时,样本率的分布近似正态分布,则总体率的可信区间可由下列公式估计:
总体率(π)的95%可信区间:p±1.96sp
总体率(π)的99%可信区间:p±2.58sp
例如前述两组高碘地方性甲状腺肿患病率的总体患病率可信区间为:
第一组:
95%可信区间为1.78%±1.96×0.23%=1.33%~2.23%
95%可信区间为1.78%±2.58×0.23%=1.19%~2.37%
第二组:
95%可信区间为5.6%±1.96×0.41%=4.80%~6.40%
95%可信区间为5.6%±2.58×0.41%=4.54%~6.66%
(二)查表法
当样本含量n较小,如n≤50,特别是p接近0或1时,则按二项分布原理确定总体率的可信区间,其计算较繁,读者可根据样本含量n和阳性数X参照专用统计学介绍的二项分布中95%可信限表。
| Copyright @ 2002-2010 婵犵數濮烽弫鎼佸磻閻愬搫鍨傞柛顐f礀缁犲綊鏌嶉崫鍕櫣闁稿被鍔戦弻銈吤圭€n偅鐝掗梺缁樺笒閿曨亪寮婚敐鍛傛棃鍩€椤掑嫭鍋嬮煫鍥ㄧ☉閻撴繈鏌¢崘锝呬壕闂侀潧娲ょ€氫即鐛鈧、娑樜旈埀顒佺閸撗€鍋撶憴鍕婵炲眰鍨藉畷鎴﹀箛椤斿墽锛濋梺绋挎湰閻熝囁囬敂濮愪簻闁挎棁妫勯婊堟煙缁涘浜版慨濠冩そ瀹曨偊宕熼鐘辩礃闂備礁鎽滄慨鐢稿箰閹灛锝夊箛閺夎法鐫勯梺鍓插亞閸犳劕鈻嶉姀銈嗏拺閻犳亽鍔屽▍鎰版煙閸戙倖瀚�. xxmy.com 闂傚倸鍊搁崐鐑芥嚄閸撲礁鍨濇い鏍亼閳ь剙鍟村畷銊р偓娑櫭禍杈ㄧ節閻㈤潧孝闁稿﹤顕槐鎾愁潩閼哥數鍘卞銈嗗姉婵挳宕濆杈╃<闁绘﹩鍠栭崝锕傛煛鐏炵晫啸妞ぱ傜窔閺屾盯骞樼捄鐑樼€诲銈嗘穿缂嶄線骞冩禒瀣窛濠电姴鍟鐔兼⒒娴h姤纭堕柛锝忕畵楠炲繘鏁撻敓锟� 濠电姷鏁告慨鐑藉极閸涘﹥鍙忔い鎾卞灩绾惧鏌熼崜褏绡€缂佽妫濋弻鏇㈠醇濠靛洤顦╅梺鎼炲€栧Σ鍫濃攽閻樺灚鏆╁┑顔诲嵆瀹曡绺介崜鍙夋櫓闂佸湱澧楀妯肩不椤栫偞鐓ラ柣鏇炲€圭€氾拷10017704闂傚倸鍊搁崐椋庣矆娓氣偓楠炲鏁撻悩鍐蹭画闂備緡鍓欑粔瀵哥不椤栫偞鐓ラ柣鏇炲€圭€氾拷 |