第三节 可信区间的估计
一、参数估计的意义
一组调查或实验数据,如果是计量资料可求得平均数,标准差等统计指标,如果是计数资料则求百分率藉以概括说明这群观察数据的特征,故称特征值。由于样本特征值是通过统计求得的,所以又称为统计量以区别于总体特征值。总体特征值一般称为参数(总体量)。我们进行科研所要探索的是总体特征值即总体参数,而我们得到的却是样本统计量,用样本统计量估计或推论总体参数的过程叫参数估计。
本章第一节例6.1通过检查110个健康成人的尿紫质算得阳性率为10%,这是样本率,可用它来估计总体率,说明健康成人的尿紫质阳性率水平,这样的估计叫“点估计”。但由于存在抽样误差,不同样本(如再检查110人)可能得到不同的估计值。因此我们常用“区间估计”总体率(或总体均数)大概在那一个范围内,这个范围就叫可信区间。区间小的一端叫下限,大的一端叫上限。常用的有95%可信区间与99%可信区间。根据同一资料所作95%可信区间比99%可信区间窄些(上、下限较靠近),但估计错误的概率后者为1%,前者为5%,进行总体参数的区间估计时可根据研究目的与标准误的大小选用95%、或99%。
二、总体均数的估计
为了说明常用的总体均数之区间估计法,我们不妨回顾一下上节所叙的t分布。
由求t的基本公式
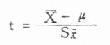
我们看到X与μ的距离等于t(SX),又根据X集中分布在μ周围的特点,若取t的5%
界即t0.05,,(或1%界)乘以SX作为X与μ的距离范围,就可用式(6.6)或式(6.7)求
出区间来估计总体均数μ所在范围,估错的概率仅有5%或1%,因此称95%或99%可信区间。下面用实例说明其求法。
95%可信区间 X-t0.05,νSX<μ
99%可信区间 X-t0.05,νSX<μ
例6.2 上面抽样实验中第1号样本的均数为488.6,标准差为61.65,例数10,自由度ν=10-1=9,试求95%与99%可信区间。
1.求标准误
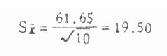
95%可信区间 488.6-2.262(19.50)<μ<488.6+2.262(19.50),即有95%的把握估计μ是在444.49~532.71区间内
99%可信区间 488.6-3.250(19.50)<μ<488.6+3.250(19.50),可有99%的把握估计μ是在425.22~551.98区间内
这里两个可信区间都包含μ=500在内,所以这次估计是估计对了。
抽样实验共抽了100个样本,除1号样本外其余99个样本均数也对μ作了区间估计,这些95%可信区间列在表6.4中。我们看到,只有5个95%可信区间(右上角标有星号)不包含总体均数μ=500在内,它们是:
| 样本号 |
X |
95%可信区间 |
| 6 |
546.7 |
515.78~577.62 |
| 7 |
524.5 |
500.45~548.55 |
| 28 |
476.1 |
454.91~497.29 |
| 72 |
465.3 |
447.02~483.58 |
| 75 |
526.6 |
503.10~550.10 |
平时我们并不重复抽取许多样本来一次次估计总体均数而仅是一次,至于算出的均数会类似一百个样本均数中的那一个就很难说了。如果不遇到类似上列那些均数过大或过小的样本,求出可信区间后总体均数真是在该区间内,那么便是一次成功的估计:但是极少数情况下我们也会遇到极端的样本,以至总体均数并不在我们提出的区间内。不过,我们具体所作的这次估计到底属于前种情况还是后一种,这是无法知道的,因为我们不知道μ是多少(若已知μ便不必估计它了)。然而象后种情况那样作出错估的概率终究很小,只5%或1%,所以用这样的方法估计总体均数还是可行的。
三、总体率的估计
上面已经提到,计数资料可以计算相对数(率)。我们若由样本统计量P估计总体参数π,同样要考虑率的抽样误差,据数理统计研究结果,样本率的分布也近似正态分布,尤其当π比较靠近50%且样本较大时。于是对样本,百分率的可信区间可利用正态分布规律估计,公式是:
95%可信区间 P-1.96Sp<π
99%可信区间 P-2.58Sp<π
(按正态分布,双侧尾部面积α=0.05时的u值为1.96,α=0.01时的u值为2.58,故用这两式求可信区间时不必查表找临界u值,记住这两数即可。)
例6.3 某医院收治200例急性菌痢患者,其中粪便细菌培养阳性者共80例,试估计菌痢细菌培养的总体阳性率95%与99%可信区间。
1.求阳性率 P=80/200×100%=40% (或0.40)
2.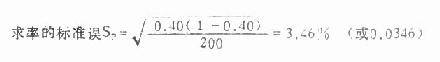
3.求可信区间
95%可信区间 40%-1.96(3.46%)<π<40%+1.96(3.46%),即估计π在33.22%~46.78%之间
99%可信区间 40%-2.58(3.46%)<π<40%+2.58(3.46%),即估计π在31.07%~48.93%之间
如果是小样本的百分率,求可信区间可通过查表获得,附表4是n为10、15、20、30时查95%与99%可信区间的一个简表。此外,统计学专著中还有更详细的表可查。
(俞元春编)